Significant Figures Rules Addition Subtraction Multiplication Division

When you multiply or divide you assign significant figures in the answer based on the smallest number of significant figures from your original set of measurements.
Significant figures rules addition subtraction multiplication division. Any zeros between two significant digits are significant. So let me add those up. Convert 23 c 2 significant figures to k kelvin k 273 15 º c 296 15 296 k 23. For multiplication and division however it is the number of sig figs but not the place value that matters.
For addition and subtraction use the following rules. Focus on these rules and learn them well. For multiplication and division only the total number of significant figures in each of the factors matters. Non zero digits are always significant.
You d add the 1 901 plus the 2 09. The rules for calculating significant figures for multiplication and division are opposite to the rules for addition and subtraction. Provide the number of sig figs in each of the following numbers. Notice the difference between the two rules.
The final answer limited to four significant figures is 4 094. The subtraction of 73 32 yields 41 which contains 2 significant figures. Rules for combined addition subtraction and multiplication division problems first apply the rules for addition subtraction determine the number of sig figs for that step then apply the rules for multiplication division. There are three rules on determining how many significant figures are in a number.
When you add or subtract you assign significant figures in the answer based on the number of decimal places in each original measurement. Well if you didn t care about significant figures or precision you would just add them up. For multiplication or division the rule is to count the number of significant figures in each number being multiplied or divided and then limit the significant figures in the answer to the lowest count. You can t make imprecise numbers more precise just by combining them with ones that already are.
Both 10 1 and 1 07 have 3 sig figs. So you get 3 991. So for the number 113 9177 etc you would round to the least number of sig figs in the problem. A final zero or trailing zeros in the decimal portion only are significant.
Count the number of significant figures in the decimal portion only of each number in the problem add or subtract in the normal fashion your final answer may have no more significant figures to the right of the decimal than the least number. Remember for addition or subtraction report to the same number of decimal places as the term with the least amount of decimal places see rule 5. The first digit dropped is 1 so we do not round up. The decimal place of the last significant figure in each factor is irrelevant.
However the rule for addition and subtraction is not the same as for multiplication and division. For addition and subtraction we round to the least precise place value. An example is as follows. That s why rules exist for mathematical operations with numbers of different precision and these rules are based on significant digits.

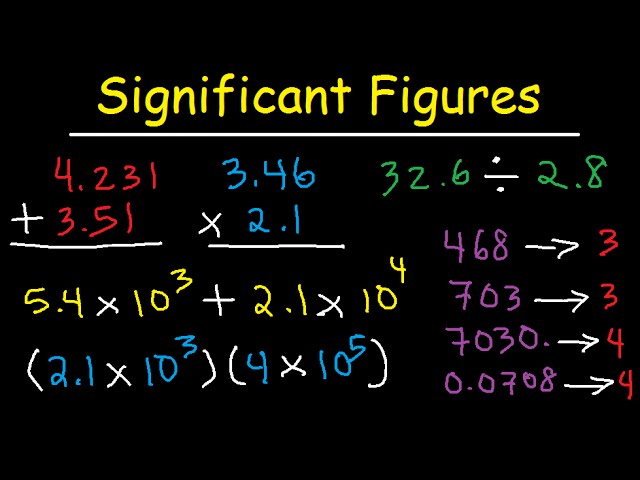















.PNG)
